Gravitational and teconic forces controlling post-collisional deformation and the present-day stress field of the Alps. Constraints from numerical modelling
(pdf)
We perform numerical modelling to investigate the
mechanisms leading to the post-collisional tectonic evolution of
Alps. We model the lithospheric deformation as a viscous thin-sheet
with vertically-averaged rheology and coupled with surface mass
transport. The applied kinematic boundary conditions simulate the
convergence between the Adria indenter and the European foreland
during the last 35 Ma. Model predictions of elevation, lithospheric
structure, erosion/sedimentation pattern and vertical-axis rotation
are compared with observations of the planform shape of the chain,
topography, crustal thickness, distribution of rock exhumation and
sediment thickness, and paleomagnetic rotations.
Thickening of the lithosphere in the Alpine region is shown to be
highly sensitive to the assumed viscosity law, to the strength contrasts
between the different regions and to the surface mass transport.
Modelling results indicate that the large-scale deformation of the
Alps during the post-collisional phase is mainly controlled by accommodation
of convergence in a weak orogenic zone caught between a nearly rigid
Adria plate and a strong European foreland.
Modelling of the present-day stress field shows that: 1) the present
rotation of Adria is responsible for the change of extension direction
from strike-perpendicular in the western Alps to strike-parallel
in the east; and 2) the strike-perpendicular extension observed
in the western Alps is likely due to lateral variations of gravitational
potential energy. The results suggest a NNE shift of about 700 km
of the Euler pole of Adria relative to Europe from its mean position
during post-collisional deformation to the present-day.
|
|
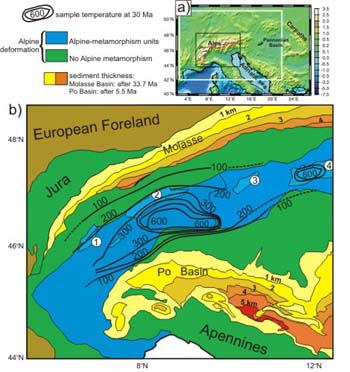

a) Topography of the Alpine region and location of the modelling
area (white rectangle) and of the geologic map (black rectangle);
b) Geologic map of the study area showing temperature of metamorphic
rock samples (black contours, in °C; every 100°C would imply
exhumation between 3 and 5 km) at approximately 30 Ma. Yellow/orange
colours show sediment thickness in the Molasse (Oligocene to present)
and Po basins (Pliocene to present). Numbers in circles identify
the following geological units: 1: Mont Blanc/Aiguilles Rouges massif;
2: Aar Massif; 3: Engadine Window; and 4: Tauern Window.
|
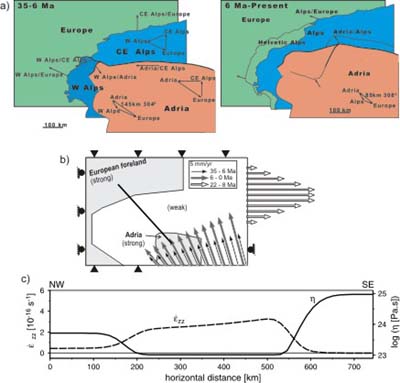

a) Restoration of displacements in the Alps in terms of the relative
motions of discrete terrains. Displacement estimates are from
Platt (1986) and Menard et al. (1991). b) Model set-up showing
the initial geometry and applied boundary conditions from 35 to
6 Ma (black solid arrows) and from 6 Ma to present (grey arrows).
White arrows at the eastern boundary represent the opening of
the Pannonian basin in the period from 22 to 8 Ma. The model domain
is 1500x1000 km, and corresponds to the area between (2.2 E, 41.8
N) and (22 E, 51 N). c) Initial effective viscosity and resulting
vertical strain rate along a NW-SW profile located in Figure 3b.
|
|
|
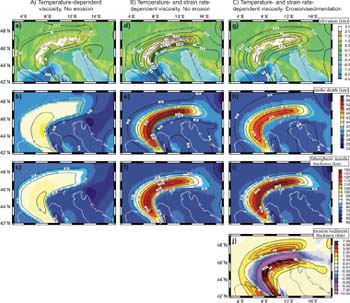
 Model results at the last stage (35 Myr, corresponding to the present)
for Model A (first column): temperature-dependent viscosity and
constant effective strain rate of 4 10-16 s-1 thorough the entire
model domain; Model B (second column): temperature- and strain rate-dependent
viscosity; Model C (third column): as B but incorporating erosion
and sedimentation, Kd=1000 m2/yr. Upper panels show the actual topography
in the study area (color shading) and the model-predicted topography
(contours). Central and lower panels show the predicted Moho depth
and lithospheric mantle thickness. Lowermost-right panel shows the
amount of erosion/sedimentation predicted in Model C (negative values
for erosion and positive for sedimentation). Note that the three
models incorporate the same boundary conditions, and therefore the
same amount of mass input and total lithospheric shortening. Differences
in topography and thickness distributions are due exclusively to
the different rheology assumed (compare models A and B) and to the
effects of surface transport (compare models B and C).
Model results at the last stage (35 Myr, corresponding to the present)
for Model A (first column): temperature-dependent viscosity and
constant effective strain rate of 4 10-16 s-1 thorough the entire
model domain; Model B (second column): temperature- and strain rate-dependent
viscosity; Model C (third column): as B but incorporating erosion
and sedimentation, Kd=1000 m2/yr. Upper panels show the actual topography
in the study area (color shading) and the model-predicted topography
(contours). Central and lower panels show the predicted Moho depth
and lithospheric mantle thickness. Lowermost-right panel shows the
amount of erosion/sedimentation predicted in Model C (negative values
for erosion and positive for sedimentation). Note that the three
models incorporate the same boundary conditions, and therefore the
same amount of mass input and total lithospheric shortening. Differences
in topography and thickness distributions are due exclusively to
the different rheology assumed (compare models A and B) and to the
effects of surface transport (compare models B and C).
|
|
|
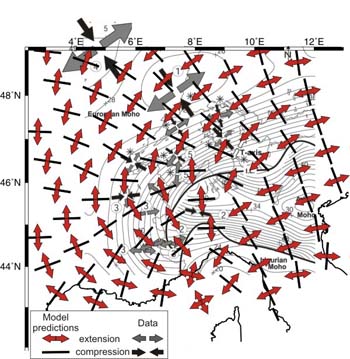

Horizontal components of the principal strain rate directions, predicted
by thin-sheet Model C (black bars for compression and white arrows
for extension) and measures compiled by Kastrup et al. (2004) (black
arrows for compression and grey arrows for extension). Contours
are Moho depth, with 2 km interval (Waldhauser et al., 2002).
|
|

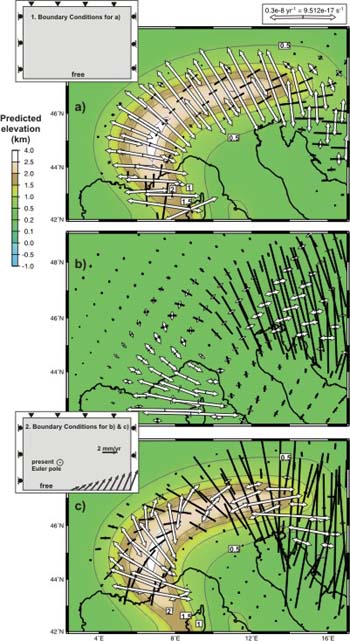
Horizontal components of the principal strain rate tensor predicted
for the last stage (present day) of Model C (arrows for extension
and bars for compression). Insets: 1 corresponds to the boundary
condition without Adria movement and applied on panel a); and 2
present rotation of Adria, the velocity boundary conditions are
computed assuming an Euler pole from a geodetic study and applied
on panels b) and c). The strain rates are obtained considering:
a) the only driving force comes from lateral variations of GPE,
no Adria convergence (inset 1); b) by applying in an homogeneous
lithosphere (no lateral variations of crustal and lithospheric thickness,
therefore, no lateral contrast of GPE) a velocity boundary condition
computed from the present Euler pole (inset 2); and c) by applying
to the last stage (including the lateral variations of GPE) the
velocity boundary condition computed from the same Euler pole (inset
2). Contours correspond to the predicted elevation.
The present-day strike-perpendicular extension observed in the
western Alps can be explained as driven by lateral variations of
GPE in this area. Ongoing rotation of Adria relative to Europe causes
the observed rotation of extension direction from perpendicular
to the chain in the western Alps to parallel to it in the eastern
Alps. In this way, we obtain a change in tectonic regime from normal-faulting
in the southwestern Alps to thrusting in the eastern Alps. Whereas
explaining this present stress regime requires a rotation pole similar
to that derived from geodetic measurements (9.10°E, 45.36°N),
a rotation pole further to the south (7.1°E,39.3°N) is needed
to reproduce the distribution of mean post-collisional Alpine deformation.
Consequently, we propose that the Euler pole of Adria (relative
to Europe) has shifted NNE-ward about 700 km from the location responsible
for mean post-collisional deformation to the present-day situation.
|
|




